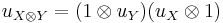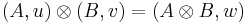Centre (category)

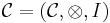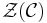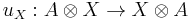Let $\mathcal{C} = (\mathcal{C},\otimes,I)$ be a (strict) monoidal category. The centre of $\mathcal{C}$ , denoted $\mathcal{Z(C)}$ , is the category whose objects are pairs (A,u) consisting of an object A of $\mathcal{C}$ and a natural isomorphism $u_X:A \otimes X \rightarrow X \otimes A$ satisfying

$u_{X \otimes Y} = (1 \otimes u_Y)(u_X \otimes 1)$

and

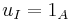$u_I = 1_A$ (this is actually a consequence of the first axiom).

An arrow from (A,u) to (B,v) in 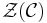$\mathcal{Z(C)}$ consists of an arrow 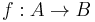$f:A \rightarrow B$ in $\mathcal{C}$ such that

$v_X (f \otimes 1_X) = (1_X \otimes f) u_X$ .

The category 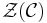$\mathcal{Z(C)}$ becomes a braided monoidal category with the tensor product on objects defined as

$(A,u) \otimes (B,v) = (A \otimes B,w)$

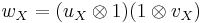where $w_X = (u_X \otimes 1)(1 \otimes v_X)$ , and the obvious braiding .

References

André Joyal and Ross Street. Tortile Yang-Baxter operators in tensor categories, J. Pure Appl. Algebra 71 (1991): 43–51.